Current sensor transfer impedance determination method: Difference between revisions
No edit summary |
No edit summary |
||
| (13 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
= Theory = | |||
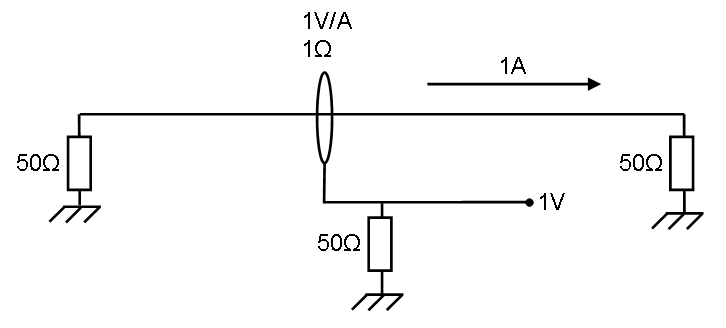
[[Image:Current sensor Transfer impedance Prove.PNG]] | [[Image:Current sensor Transfer impedance Prove.PNG]] | ||
The left impedance is the signal generator which is generating enough power for 1 ampere. | |||
This 1Amp. generates <math>P = I^2*R=50 \ Watt</math> in the right impedance. | |||
The current sensor has 1 ohm transfer impedance, this means 1 ampere generates 1 Volt on the measuring part below. | |||
The power in the lower 50 ohm impedance is <math>P = \frac{U^2}{R} = 20 \ mWatt</math> | |||
So 1 ohm: <math>10*^{10}log(\frac{0,02}{50}) \approx -33,98 dB = -20*^{10}log(50)</math> | |||
= Reference measurement = | |||
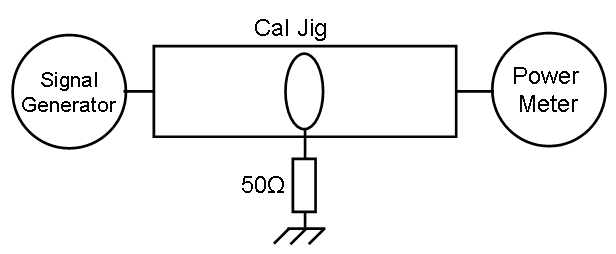
[[Image:Current sensor Transfer impedance Ref measurement.PNG]] | [[Image:Current sensor Transfer impedance Ref measurement.PNG]] | ||
= Probe measurement = | |||
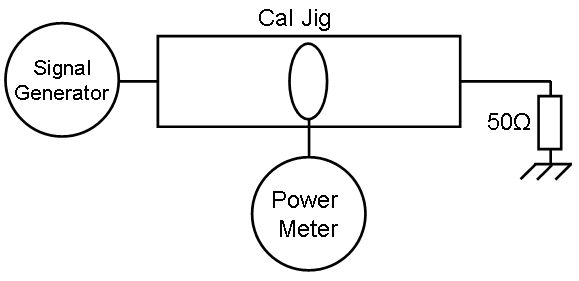
[[Image:Current sensor Transfer impedance final measurement.PNG]] | [[Image:Current sensor Transfer impedance final measurement.PNG]] | ||
= Calculation = | |||
<Math>Correction \ factor (dB)= P_{Measured} - P_{Reference}+ 33.98</Math> | |||
<Math>P_{Measured}</Math> and <Math>P_{Reference}</Math> in dBm. | |||
= Example = | |||
On 10 MHz we have the following information: | |||
*Calibration: 0 dBm. | |||
*Measurement: -27,96 dBm. | |||
So: | |||
<math>Imp.=-27,96-0.00+33.98=6,02 dBOhm</math> | |||
<math>Imp.\approx 2 \ Ohm</math> | |||
== Verification == | |||
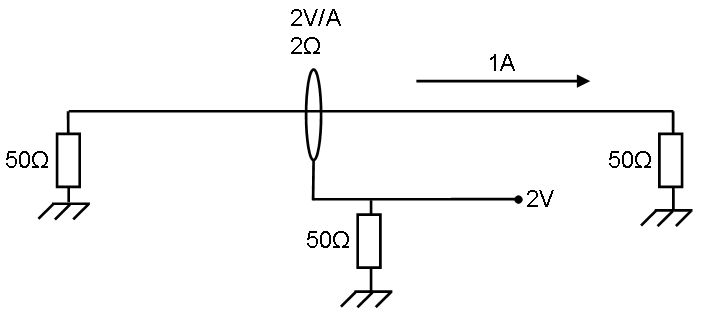
[[Image:Current sensor Transfer impedance example.png]] | |||
The left impedance is the signal generator which is generating enough power for 1 ampere. | |||
This 1 Ampere generates <math>P = I^2*R=50 \ Watt</math> in the right impedance. | |||
The current sensor has 2 ohm transfer impedance, this means 1 ampere generates 2 Volt on the measuring part below. | |||
The power in the lower 50 ohm impedance is <math>P = \frac{U^2}{R} = 80 \ mWatt</math> | |||
So 2 ohm: <math>10*^{10}log(\frac{0,08}{50}) \approx -27,96 dB</math> | |||
The difference to a 1 Ohm impedance is <math>-27,96 - (-33,98) = 6,02 dB</math> | |||
==Conclusion== | |||
Correction to a 1 ohm impedance is <math>20*^{10}log(R_{probe})</math> | |||
{{note|This method is not a replacement for a real calibration as it may be performed by a none traceable device}} | |||
[[Category:RadiMation]] | |||
Latest revision as of 07:47, 31 July 2014
Theory[edit]
The left impedance is the signal generator which is generating enough power for 1 ampere.
This 1Amp. generates in the right impedance.
The current sensor has 1 ohm transfer impedance, this means 1 ampere generates 1 Volt on the measuring part below.
The power in the lower 50 ohm impedance is
So 1 ohm:
Reference measurement[edit]
Probe measurement[edit]
Calculation[edit]
and in dBm.
Example[edit]
On 10 MHz we have the following information:
- Calibration: 0 dBm.
- Measurement: -27,96 dBm.
So:
Verification[edit]
The left impedance is the signal generator which is generating enough power for 1 ampere.
This 1 Ampere generates in the right impedance.
The current sensor has 2 ohm transfer impedance, this means 1 ampere generates 2 Volt on the measuring part below.
The power in the lower 50 ohm impedance is
So 2 ohm:
The difference to a 1 Ohm impedance is
Conclusion[edit]
Correction to a 1 ohm impedance is
| Note: | This method is not a replacement for a real calibration as it may be performed by a none traceable device |