Testlevel VSWR: Difference between revisions
Tag: Manual revert |
|||
| (8 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
{{Menu|Description|}} The description of the input. | {{Menu|Description|}} The description of the input. | ||
==== Calculation ==== | ===== Calculation ===== | ||
The VSWR (Voltage Standing Wave Ratio) test level in RadiMation is a measurement that indicates how well the energy from a signal source is being transferred to a device under test. It provides insight into the efficiency of power delivery, with a lower VSWR indicating better efficiency and minimal energy reflection. This is important in electromagnetic immunity testing to ensure accurate power application across test frequencies. | The VSWR (Voltage Standing Wave Ratio) test level in RadiMation is a measurement that indicates how well the energy from a signal source is being transferred to a device under test. It provides insight into the efficiency of power delivery, with a lower VSWR indicating better efficiency and minimal energy reflection. This is important in electromagnetic immunity testing to ensure accurate power application across test frequencies. | ||
In RadiMation, the VSWR is calculated based on the Return Loss (RL) between the forward power and reflected power. | In RadiMation, the VSWR is calculated based on the Return Loss (RL) between the forward power and reflected power. | ||
* Calculate Return Loss (RL): | * Calculate Return Loss (RL): | ||
<math> RL = P_{fwd} - P_{refl} </math> | |||
In RadiMation, this is calculated as the difference between the forward power and the reflected power. | In RadiMation, this is calculated as the difference between the forward power and the reflected power. | ||
* Calculate the Reflection Coefficient: | * Calculate the Reflection Coefficient: | ||
<math> \Gamma = 10^{\frac{-RL}{20}} </math> | |||
The reflection coefficient is a value derived from the Return Loss. It quantifies the proportion of energy reflected from the device. | The reflection coefficient is a value derived from the Return Loss. It quantifies the proportion of energy reflected from the device. | ||
* Calculate VSWR: | * Calculate VSWR: | ||
<math> VSWR = \frac{1 + \Gamma}{1 - \Gamma} </math> | |||
If the reflection coefficient is 1 (meaning full reflection with no power transfer), the VSWR is set to a high value (e.g., 1000) to represent an infinite VSWR. | If the reflection coefficient is 1 (meaning full reflection with no power transfer), the VSWR is set to a high value (e.g., 1000) to represent an infinite VSWR. | ||
VSWR measures the standing wave pattern created by the interference between the forward and reflected waves. It’s calculated based on the reflection coefficient as follows: | |||
[[Category:Manual]] | [[Category:Manual]] | ||
Latest revision as of 12:44, 15 November 2024
Input Test level: VSWR[edit]
-
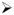 Description The description of the input.
Description The description of the input.
-
Calculation[edit]
The VSWR (Voltage Standing Wave Ratio) test level in RadiMation is a measurement that indicates how well the energy from a signal source is being transferred to a device under test. It provides insight into the efficiency of power delivery, with a lower VSWR indicating better efficiency and minimal energy reflection. This is important in electromagnetic immunity testing to ensure accurate power application across test frequencies.
In RadiMation, the VSWR is calculated based on the Return Loss (RL) between the forward power and reflected power.
- Calculate Return Loss (RL):
In RadiMation, this is calculated as the difference between the forward power and the reflected power.
- Calculate the Reflection Coefficient:
The reflection coefficient is a value derived from the Return Loss. It quantifies the proportion of energy reflected from the device.
- Calculate VSWR:
If the reflection coefficient is 1 (meaning full reflection with no power transfer), the VSWR is set to a high value (e.g., 1000) to represent an infinite VSWR. VSWR measures the standing wave pattern created by the interference between the forward and reflected waves. It’s calculated based on the reflection coefficient as follows: