RadiMation Application Note 161: Difference between revisions
| (39 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
=== The relation between ERP and EIRP === | === The relation between ERP and EIRP === | ||
The relationship between ERP and EIRP is generally: | The relationship between ERP and EIRP is generally: | ||
<math>\text{EIRP (dBm)} = \text{ERP (dBm)} + 2.15 \ \text{dB}</math> | |||
<math>\text{ERP (dBm)} = \text{EIRP (dBm)} - 2.15 \ \text{dB}</math> | |||
Here, the 2.15 dB accounts for the difference in gain between an ideal isotropic antenna and an ideal dipole antenna. | Here, the 2.15 dB accounts for the difference in gain between an ideal isotropic antenna and an ideal dipole antenna. | ||
this difference is: | this difference is: | ||
<math>\text{Linear factor: } 1.6409224</math> | |||
<math>\text{Logarithmic factor: } 10 \times \log_{10}(1.6409224) = 2.15088 \approx 2.15</math> | |||
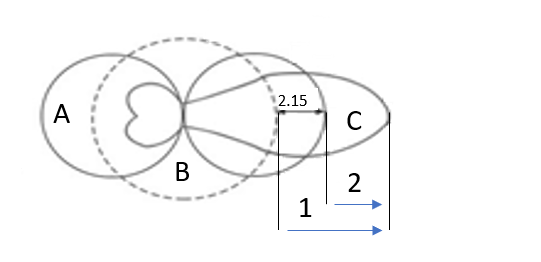
[[File: Isotropic_dipole_gain.png]] | |||
{{ScreenElementDescription|A|Ideal dipole radiator antenna diagram.}} | |||
{{ScreenElementDescription|B|Ideal isotropic radiator antenna diagram.}} | |||
{{ScreenElementDescription|C|Practical antenna diagram.}} | |||
{{ScreenElementDescription|1|Gain relative to isotropic antenna.}} | |||
{{ScreenElementDescription|2|Gain relative to dipole antenna.}} | |||
For more information see the following article [https://en.wikipedia.org/wiki/Gain_(antenna)#Second_example Gain] | |||
=== Relativity in Antenna Types === | |||
'''Isotropic Antenna''': An ideal, theoretical antenna that radiates power uniformly in all directions. It does not exist in reality but serves as a reference. | |||
'''Dipole Antenna''': A real-world antenna with directionality. | |||
Since isotropic antennas are only theoretical, actual real-world measurements can be referenced back to a dipole, making ERP a representative of real-world scenarios. | |||
=== Measuring === | === Measuring === | ||
When measurements are taken in an anechoic chamber, the power received by the receiver is typically in the direction of the main lobe of the antenna, representing the power radiated in that specific direction. To calculate EIRP, the measured power is adjusted by the gain of the antenna in that direction relative to an isotropic radiator. | When measurements are taken in an anechoic chamber, the power received by the receiver is typically in the direction of the main lobe of the antenna, representing the power radiated in that specific direction. To calculate EIRP, the measured power is adjusted by the gain of the antenna in that direction relative to an isotropic radiator. | ||
If the reference antenna is a dipole, the result is expressed as ERP. | If the reference antenna is a dipole, the result is expressed as ERP. | ||
==== RadiMation Software and Real-World Measurements ==== | ==== RadiMation Software and Real-World Measurements ==== | ||
| Line 48: | Line 62: | ||
If the measurement is done with RadiMation with a certain antenna at a certain distance the definition or EIRP and ERP would become: | If the measurement is done with RadiMation with a certain antenna at a certain distance the definition or EIRP and ERP would become: | ||
EIRP represents the equivalent power that would have been radiated by an equivalent isotropic antenna to achieve the same power density at a particular point in a specific direction as the actual antenna does. | |||
and | and | ||
ERP represents the effective power that is radiated by an equivalent dipole antenna to achieve the measured power density a particular point in a specific direction. | |||
The measurement itself in the chamber doesn’t inherently provide EIRP or ERP results it just measures the radiated power at a specified distance in a given direction(often the main lobe). | The measurement itself in the chamber doesn’t inherently provide EIRP or ERP results it just measures the radiated power at a specified distance in a given direction(often the main lobe). | ||
| Line 58: | Line 72: | ||
As an isotropic antenna radiates across a sphere, the following formula: | As an isotropic antenna radiates across a sphere, the following formula: | ||
<math>A = 4 \pi R^2 </math> | <math>A = 4 \pi R^2 </math> | ||
A: Area | |||
R: Distance from the transmitter. | |||
can be used to calculate the area over which the measured power is divided resulting in the power density(w/m2) result. | can be used to calculate the area over which the measured power is divided resulting in the power density(w/m2) result. | ||
<math>P_D = \frac{P_t}{4 \pi R^2}</math> | <math>P_D = \frac{P_t}{4 \pi R^2}</math> | ||
PD: Power density at a distance R from the transmitter. | |||
Pt: Transmitter power. | |||
R: Distance from the transmitter. | |||
Applying this formula thus results in the power density emitted by the isotropic antenna at the given distance based on the transmitter power. | Applying this formula thus results in the power density emitted by the isotropic antenna at the given distance based on the transmitter power. | ||
as the Gain (G) of an antenna is the ratio of power radiated in the desired direction as compared to the power radiated from an isotropic antenna | as the Gain (G) of an antenna is the ratio of power radiated in the desired direction as compared to the power radiated from an isotropic antenna | ||
<math>G = \frac{\text{Maximum radiation intensity of actual antenna}}{\text{Radiation intensity of isotropic antenna with same power input}}</math> | <math>G = \frac{\text{Maximum radiation intensity of actual antenna}}{\text{Radiation intensity of isotropic antenna with same power input}}</math> | ||
G: Gain of the antenna. | G: Gain of the antenna. | ||
Maximum radiation intensity of actual antenna: The highest radiation intensity in a specific direction produced by the actual antenna. | Maximum radiation intensity of actual antenna: The highest radiation intensity in a specific direction produced by the actual antenna. | ||
Radiation intensity of isotropic antenna with same power input: The radiation intensity that an ideal isotropic antenna would produce if it had the same input power as the actual antenna. An isotropic antenna radiates equally in all directions. | Radiation intensity of isotropic antenna with same power input: The radiation intensity that an ideal isotropic antenna would produce if it had the same input power as the actual antenna. An isotropic antenna radiates equally in all directions. | ||
The formula can be extended to use the gain of the antenna " | The formula can be extended to use the gain of the antenna " | ||
<math>P_D = \frac{P_t G_t}{4 \pi R^2}</math> | <math>P_D = \frac{P_t G_t}{4 \pi R^2}</math> | ||
PD: Power density at a distance | PD: Power density at a distance R from the transmitter. | ||
Pt: Transmitter power. | |||
Gt: Gain of the transmitting antenna. | |||
R: Distance from the transmitter. | |||
Applying this formula thus results in the power density emitted by the antenna with a specified gain at the given distance based on the transmitter power. | Applying this formula thus results in the power density emitted by the antenna with a specified gain at the given distance based on the transmitter power. | ||
This formula can be rewritten to calculate the required transmitter power by dividing the total power emitted, based on the measured power density at the given distance, with the linear gain of the antenna. | This formula can be rewritten to calculate the required transmitter power by dividing the total power emitted, based on the measured power density at the given distance, with the linear gain of the antenna. | ||
<math>P_t G_t = P_D \times 4 \pi R^2 </math> | <math>P_t G_t = P_D \times 4 \pi R^2 </math> | ||
PD: Power density at a distance | PD: Power density at a distance R from the transmitter. | ||
R: Distance from the transmitter where the power density is measured. | |||
Pt: Transmitter power, or the total power emitted by the antenna. | |||
Gt: Gain of the transmitting antenna. | |||
Use of the gain in this formula corrects the isotropic determined power density to the real antenna | Use of the gain in this formula corrects the isotropic determined power density to the real antenna | ||
The transmitter power can then be expressed in dBm. The ERP can then stated to be: | The transmitter power can then be expressed in dBm. The ERP can then stated to be: | ||
| Line 103: | Line 143: | ||
<math>\text{EIRP} = \text{ERP} + \text{2.15}</math> | <math>\text{EIRP} = \text{ERP} + \text{2.15}</math> | ||
Conclusion: | === Conclusion === | ||
[[file:EIRP-linkbudget.png]] | |||
<math>\text{ERP} = \text{Transmitter Power} + \text{Antenna Gain} + \text{Path Losses}</math> | |||
The main takeaway is that while EIRP and ERP are related, they serve to reference antenna power relative to two different idealized antenna models (theoretical-> isotropic vs. practical -> dipole). | The main takeaway is that while EIRP and ERP are related, they serve to reference antenna power relative to two different idealized antenna models (theoretical-> isotropic vs. practical -> dipole). | ||
| Line 112: | Line 155: | ||
It seems that these values could also be recalculated into ERP/EIRP outside of the software by using the power measurements from the software and converting them to isotropic power density result by taking the specified antenna distance in consideration. | It seems that these values could also be recalculated into ERP/EIRP outside of the software by using the power measurements from the software and converting them to isotropic power density result by taking the specified antenna distance in consideration. | ||
=== Additional links === | |||
[https://en.wikipedia.org/wiki/Gain_(antenna)#Second_example Gain] | |||
[https://en.wikipedia.org/wiki/Dipole_antenna#Half-wave_antenna Dipole-antenna] | |||
Latest revision as of 13:05, 25 November 2024
Information regarding EIRP and ERP[edit]
EIRP[edit]
EIRP (Equivalent Isotropically Radiated Power): This is the power that would have to be radiated by an isotropic antenna (which radiates equally in all directions) to produce the same power density in a particular direction as the actual antenna.
ERP[edit]
ERP (Effective Radiated Power): This is the power that would have to be radiated by a half-wave dipole antenna to achieve the same power density as the actual antenna in a particular direction.
The relation between ERP and EIRP[edit]
The relationship between ERP and EIRP is generally:
Here, the 2.15 dB accounts for the difference in gain between an ideal isotropic antenna and an ideal dipole antenna. this difference is:
| Ideal dipole radiator antenna diagram. |
| Ideal isotropic radiator antenna diagram. |
| Practical antenna diagram. |
| Gain relative to isotropic antenna. |
| Gain relative to dipole antenna. |
For more information see the following article Gain
Relativity in Antenna Types[edit]
Isotropic Antenna: An ideal, theoretical antenna that radiates power uniformly in all directions. It does not exist in reality but serves as a reference.
Dipole Antenna: A real-world antenna with directionality.
Since isotropic antennas are only theoretical, actual real-world measurements can be referenced back to a dipole, making ERP a representative of real-world scenarios.
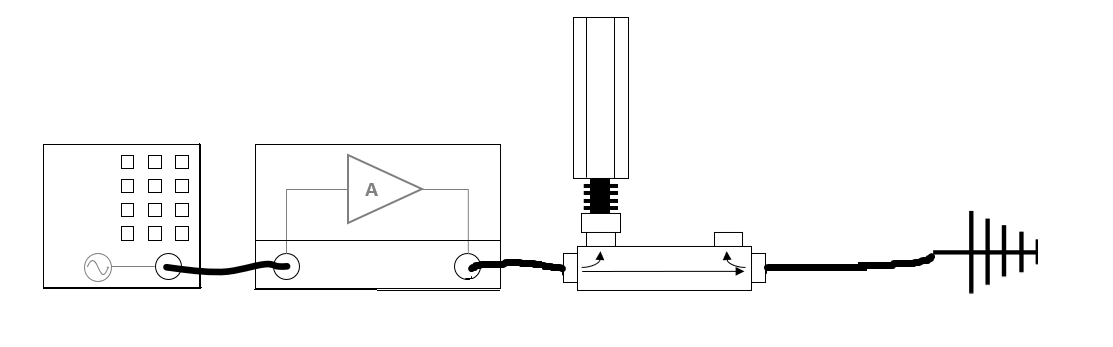
Measuring[edit]
When measurements are taken in an anechoic chamber, the power received by the receiver is typically in the direction of the main lobe of the antenna, representing the power radiated in that specific direction. To calculate EIRP, the measured power is adjusted by the gain of the antenna in that direction relative to an isotropic radiator. If the reference antenna is a dipole, the result is expressed as ERP.
RadiMation Software and Real-World Measurements[edit]
In RadiMation, when measuring with a dipole antenna in the chamber, the receiver just "sees" a signal coming from the direction of the main lobe of the transmitting dipole antenna. As far as the receiver "observes" the signal. it can be either a theoretical isotropic antenna or a directional antenna, the difference is actually not "known".
If it is known that it is a dipole, then it will be implied that the measured power is ERP, the value can then be converted to its EIRP relative counterpart.
If there would have been an actual isotropic antenna, then the measured power would be EIRP, the value can then be converted to its ERP relative counterpart.
If the power must be expressed as EIRP instead of ERP, the 2.15 dB can be added to the result (since relatively a dipole has 2.15 dB more directional gain than a theoretical equivalent isotropic antenna).
As theoretical isotropic antennas do not exist, the result would be naturally ERP because the output is measured as generated by a non-theoretical antenna (dipole). For other antennas such as for example horn antennas or log-periodic antennas, the measurements would depend on the specific characteristics of these antennas, which of course have their own gain and directivity.
It could theoretically be said that these types of antennas also have their own relative theoretical counterparts, and as these counterparts are theoretical, it also implies that real world measurement with these antennas would result in ERP results.
In theory, it could even be said that different antennas could have their own type of "ERxP scale” based on their design. However, as it stays a relative indication, it can be standardized to just ERP and EIRP which simplifies the comparison across different types of antennas.
Consideration of the distance of the measurement[edit]
If the measurement is done with RadiMation with a certain antenna at a certain distance the definition or EIRP and ERP would become:
EIRP represents the equivalent power that would have been radiated by an equivalent isotropic antenna to achieve the same power density at a particular point in a specific direction as the actual antenna does. and ERP represents the effective power that is radiated by an equivalent dipole antenna to achieve the measured power density a particular point in a specific direction.
The measurement itself in the chamber doesn’t inherently provide EIRP or ERP results it just measures the radiated power at a specified distance in a given direction(often the main lobe). This refers to the receiver not "seeing" what the antenna really is (isotropic or real)
If instead it is considered that the receiver is measuring an isotropic antenna instead, and that the measured power is thus uniform in all directions, then effectively a power density measurement is specified at that point in space, it can then be relatively stated that this power is achieved by a theoretical isotropic antenna that would have been radiating to achieve the measured power density at the given distance(m).
As an isotropic antenna radiates across a sphere, the following formula:
A: Area
R: Distance from the transmitter.
can be used to calculate the area over which the measured power is divided resulting in the power density(w/m2) result.
PD: Power density at a distance R from the transmitter.
Pt: Transmitter power.
R: Distance from the transmitter.
Applying this formula thus results in the power density emitted by the isotropic antenna at the given distance based on the transmitter power. as the Gain (G) of an antenna is the ratio of power radiated in the desired direction as compared to the power radiated from an isotropic antenna
G: Gain of the antenna.
Maximum radiation intensity of actual antenna: The highest radiation intensity in a specific direction produced by the actual antenna.
Radiation intensity of isotropic antenna with same power input: The radiation intensity that an ideal isotropic antenna would produce if it had the same input power as the actual antenna. An isotropic antenna radiates equally in all directions.
The formula can be extended to use the gain of the antenna "
PD: Power density at a distance R from the transmitter.
Pt: Transmitter power.
Gt: Gain of the transmitting antenna.
R: Distance from the transmitter.
Applying this formula thus results in the power density emitted by the antenna with a specified gain at the given distance based on the transmitter power. This formula can be rewritten to calculate the required transmitter power by dividing the total power emitted, based on the measured power density at the given distance, with the linear gain of the antenna.
PD: Power density at a distance R from the transmitter.
R: Distance from the transmitter where the power density is measured.
Pt: Transmitter power, or the total power emitted by the antenna.
Gt: Gain of the transmitting antenna.
Use of the gain in this formula corrects the isotropic determined power density to the real antenna
The transmitter power can then be expressed in dBm. The ERP can then stated to be:
and resulting its EIRP counterpart would be:
Conclusion[edit]
The main takeaway is that while EIRP and ERP are related, they serve to reference antenna power relative to two different idealized antenna models (theoretical-> isotropic vs. practical -> dipole). It seems that more calculations would have to be implemented in RadiMation to report an EIRP or ERP value. conversion of the two values can simply be done according to the conversion factor.
RadiMation currently reports a power measurement at a given point in space, which is tracked as part of the test configuration and not actively used in any calculations.
It seems that these values could also be recalculated into ERP/EIRP outside of the software by using the power measurements from the software and converting them to isotropic power density result by taking the specified antenna distance in consideration.