Fixed step count stepper: Difference between revisions
(Created page with "== Fixed step count stepper == The Fixed Count Stepper provides a way to step the frequency in a band/decade/octave with a configured number of steps. The following examples...") |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Fixed step count stepper == | == Fixed step count stepper == | ||
The | The 'fixed step count' stepper provides a possibility to step with a specific number of frequencies in a band, decade or octave. | ||
The following examples explain how to calculate the frequency step | |||
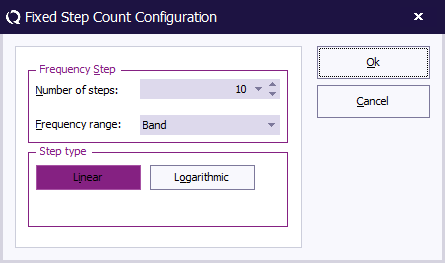
[[Image:FixedStepCountConfiguration.png]] | |||
The settings that can be configured for this stepper are: | |||
{{ScreenElementDescriptionStart}} | |||
{{ScreenElementDescription|Number of steps|Specifies the number of frequencies that are should be tested in the selected {{ScreenElement|Frequency range}}.}} | |||
{{ScreenElementDescription|Frequency range|The frequency range in which the specified {{ScreenElement|Number of steps}} should be tested. This setting can be one of:{{ScreenElementDescriptionStart}} | |||
{{ScreenElementDescription|Band|The specified number of frequencies should be used for the complete band as it is configured in the TSF file.}} | |||
{{ScreenElementDescription|Decade|The specified number of frequencies should be used in every decade (the frequency range from a frequency to the frequency that is 10x higher).}} | |||
{{ScreenElementDescription|Octave|The specified number of frequencies should be used in every octave (the frequency range from a frequency to the frequency that is 2x higher).}} | |||
}} | |||
{{ScreenElementDescriptionEnd}} | |||
{{ScreenElementDescription|Step type|If the frequencies in the selected {{ScreenElement|Frequency range}} should be distributed using a {{ScreenElement|Linear}} or {{ScreenElement|Logarithmic}} distribution.}} | |||
{{ScreenElementDescriptionEnd}} | |||
The following examples explain how to calculate the actually tested frequencies using the fixed step count stepper. | |||
<!-- Editing remark: Because the tables are passed to a template, the {{!}} should be used instead of the | --> | |||
{{Example|header=Example of linearly dividing 5 steps in a decade: | |||
|text=In a band from 100 kHz to 10 MHz, the following frequencies are tested: | |||
{{{!}}class="wikitable" | |||
! Decade range {{!}}{{!}} frequency step {{!}}{{!}} 1st {{!}}{{!}} 2nd {{!}}{{!}} 3rd {{!}}{{!}} 4th {{!}}{{!}} 5th | |||
{{!}}- | |||
{{!}} 100 kHz - 1 MHz {{!}}{{!}} (1 MHz - 100 kHz) / 5 = 180 kHz {{!}}{{!}} 100 kHz {{!}}{{!}} 280 kHz {{!}}{{!}} 460 kHz {{!}}{{!}} 640 kHz {{!}}{{!}} 820 kHz | |||
{{!}}- | |||
{{!}} 1 MHz - 10 MHz {{!}}{{!}} (10 MHz - 1 MHz) / 5 = 1.8 MHz {{!}}{{!}} 1 MHz {{!}}{{!}} 2.8 MHz {{!}}{{!}} 4.6 MHz {{!}}{{!}} 6.4 MHz {{!}}{{!}} 8.2 MHz | |||
{{!}}- | |||
{{!}} 10 MHz - 100 MHz {{!}}{{!}} (100 MHz - 10 MHz) / 5 = 18 MHz {{!}}{{!}} 10 MHz {{!}}{{!}} {{!}}{{!}} {{!}}{{!}} {{!}}{{!}} | |||
{{!}}} | |||
The start frequency of the next decade is actually part of the next decade, and thus the last 10 MHz frequency is the third decade from 10 MHz to 100 MHz, however as the stop frequency of the band is 10 MHz, only that single 10 MHz frequency is tested in the third decade. | |||
}} | |||
=== Example 1: Linearly dividing a decade in x number of steps === | === Example 1: Linearly dividing a decade in x number of steps === | ||
Suppose we have the frequency range of 1 kHz to 10 kHz, which is one full decade apart from each other. | |||
Suppose we have the frequency range of 1 kHz to 10 kHz, which is one full decade apart from each other. | |||
If we linearly divide this decade into 10 steps, we would end up with the following series: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 kHz. | If we linearly divide this decade into 10 steps, we would end up with the following series: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 kHz. | ||
=== Example 2: Stepping through a frequency range that is part of a full decade === | === Example 2: Stepping through a frequency range that is part of a full decade === | ||
Now, let's consider the frequency range of 5 kHz to 10 kHz, which is not a full decade apart from each other. | |||
Now, let's consider the frequency range of 5 kHz to 10 kHz, which is not a full decade apart from each other. | We can still perform 10 steps/decade by testing the series 5, 6, 7, 8, 9, 10 kHz, which is a linear division of the full decade from 1 kHz to 10 kHz. | ||
We can still perform 10 steps/decade by testing the series 5, 6, 7, 8, 9, 10 kHz, which is a linear division of the full decade from 1 kHz to 10 kHz. | |||
In this case, because the start frequency is higher than the start of the decade, less steps need to be tested, but it is still done based on the configured 10 steps/decade. | In this case, because the start frequency is higher than the start of the decade, less steps need to be tested, but it is still done based on the configured 10 steps/decade. | ||
=== Example 3: Using logarithmic stepping and starting frequency === | === Example 3: Using logarithmic stepping and starting frequency === | ||
Suppose we use logarithmic stepping to divide the full decade (1 kHz to 10 kHz) into 10 steps/decade. | |||
Suppose we use logarithmic stepping to divide the full decade (1 kHz to 10 kHz) into 10 steps/decade. | We might end up with a frequency series that includes a frequency value of 4.9 kHz, which is not part of the specified frequency range of 5 kHz to 10 kHz. | ||
We might end up with a frequency series that includes a frequency value of 4.9 kHz, which is not part of the specified frequency range of 5 kHz to 10 kHz. | In this case, the next frequency in the series might be 5.7 kHz, which becomes the start frequency for the test because it is the first frequency in the series that is above the configured start frequency of 5 kHz. | ||
In this case, the next frequency in the series might be 5.7 kHz, which becomes the start frequency for the test because it is the first frequency in the series that is above the configured start frequency of 5 kHz. | |||
This behavior is similar to Example 2. | This behavior is similar to Example 2. | ||
=== Example 4: Stepping through a frequency range that is not a full decade apart from each other === | === Example 4: Stepping through a frequency range that is not a full decade apart from each other === | ||
Suppose we have the frequency range of 5 kHz to 20 kHz, which is not a full decade apart from each other. | |||
If we see this frequency range as part of a full decade starting from 5 kHz to 50 kHz, where we expect to perform 10 steps/decade, we would linearly end up with the following series: 5, 10, 15, 20 kHz of frequencies to be tested. | |||
If we logarithmically divide the 10 steps over the decade from 5 kHz to 50 kHz, 5 kHz is always found in the series because it is used as the base of a decade. | |||
In RadiMation, we determine the decades based on the series 0.1, 1, 10, 100, etc. for best reproducibility. | |||
The resulting stepped frequencies will always be the same for each different "decade", regardless of the configured start frequency. Each decade is divided by the selected number of steps, after which the remaining points in the configured frequency range set by the end-user are tested. | |||
In RadiMation, we determine the decades based on the series 0.1, 1, 10, 100, etc. for best reproducibility. | |||
The resulting stepped frequencies will always be the same for each different "decade", regardless of the configured start frequency. Each decade is divided by the selected number of steps, after which the remaining points in the configured frequency range set by the end-user are tested. | |||
Therefore, if you use a Fixed Count Stepper with 10 logarithmic steps per decade and a configured start frequency of 200 Hz, the actual start frequency may be slightly different due to the logarithmic stepping. In this case, the start frequency might be 215 Hz instead of the configured 200 Hz. | Therefore, if you use a Fixed Count Stepper with 10 logarithmic steps per decade and a configured start frequency of 200 Hz, the actual start frequency may be slightly different due to the logarithmic stepping. In this case, the start frequency might be 215 Hz instead of the configured 200 Hz. | ||
Latest revision as of 10:07, 12 June 2023
Fixed step count stepper[edit]
The 'fixed step count' stepper provides a possibility to step with a specific number of frequencies in a band, decade or octave.
The settings that can be configured for this stepper are:
| Specifies the number of frequencies that are should be tested in the selected Frequency range. |
The frequency range in which the specified Number of steps should be tested. This setting can be one of:
|
| If the frequencies in the selected Frequency range should be distributed using a Linear or Logarithmic distribution. |
The following examples explain how to calculate the actually tested frequencies using the fixed step count stepper.
| “ | Example of linearly dividing 5 steps in a decade:
In a band from 100 kHz to 10 MHz, the following frequencies are tested:
The start frequency of the next decade is actually part of the next decade, and thus the last 10 MHz frequency is the third decade from 10 MHz to 100 MHz, however as the stop frequency of the band is 10 MHz, only that single 10 MHz frequency is tested in the third decade. |
” |
Example 1: Linearly dividing a decade in x number of steps[edit]
Suppose we have the frequency range of 1 kHz to 10 kHz, which is one full decade apart from each other. If we linearly divide this decade into 10 steps, we would end up with the following series: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 kHz.
Example 2: Stepping through a frequency range that is part of a full decade[edit]
Now, let's consider the frequency range of 5 kHz to 10 kHz, which is not a full decade apart from each other. We can still perform 10 steps/decade by testing the series 5, 6, 7, 8, 9, 10 kHz, which is a linear division of the full decade from 1 kHz to 10 kHz. In this case, because the start frequency is higher than the start of the decade, less steps need to be tested, but it is still done based on the configured 10 steps/decade.
Example 3: Using logarithmic stepping and starting frequency[edit]
Suppose we use logarithmic stepping to divide the full decade (1 kHz to 10 kHz) into 10 steps/decade. We might end up with a frequency series that includes a frequency value of 4.9 kHz, which is not part of the specified frequency range of 5 kHz to 10 kHz. In this case, the next frequency in the series might be 5.7 kHz, which becomes the start frequency for the test because it is the first frequency in the series that is above the configured start frequency of 5 kHz. This behavior is similar to Example 2.
Example 4: Stepping through a frequency range that is not a full decade apart from each other[edit]
Suppose we have the frequency range of 5 kHz to 20 kHz, which is not a full decade apart from each other. If we see this frequency range as part of a full decade starting from 5 kHz to 50 kHz, where we expect to perform 10 steps/decade, we would linearly end up with the following series: 5, 10, 15, 20 kHz of frequencies to be tested. If we logarithmically divide the 10 steps over the decade from 5 kHz to 50 kHz, 5 kHz is always found in the series because it is used as the base of a decade.
In RadiMation, we determine the decades based on the series 0.1, 1, 10, 100, etc. for best reproducibility. The resulting stepped frequencies will always be the same for each different "decade", regardless of the configured start frequency. Each decade is divided by the selected number of steps, after which the remaining points in the configured frequency range set by the end-user are tested.
Therefore, if you use a Fixed Count Stepper with 10 logarithmic steps per decade and a configured start frequency of 200 Hz, the actual start frequency may be slightly different due to the logarithmic stepping. In this case, the start frequency might be 215 Hz instead of the configured 200 Hz.